I. SỰ CẦN THIẾT PHẢI PHÂN TÍCH THUẬT TOÁN
Trong khi giải một bài toán chúng ta có thể có một số giải thuật khác nhau, vấn đề là cần phải đánh giá các giải thuật đó để lựa chọn một giải thuật tốt (nhất). Thông thường thì ta sẽ căn cứ vào các tiêu chuẩn sau:
Với yêu cầu (1), để kiểm tra tính đúng đắn của giải thuật chúng ta có thể cài đặt giải thuật đó và cho thực hiện trên máy với một số bộ dữ liệu mẫu rồi lấy kết quả thu được so sánh với kết quả đã biết. Thực ra thì cách làm này không chắc chắn bởi vì có thể giải thuật đúng với tất cả các bộ dữ liệu chúng ta đã thử nhưng lại sai với một bộ dữ liệu nào đó. Vả lại cách làm này chỉ phát hiện ra giải thuật sai chứ chưa chứng minh được là nó đúng. Tính đúng đắn của giải thuật cần phải được chứng minh bằng toán học. Tất nhiên điều này không đơn giản và do vậy chúng ta sẽ không đề cập đến ở đây.
Khi chúng ta viết một chương trình để sử dụng một vài lần thì y ê u cầu (2) là quan trọng nhất. Chúng ta cần một giải thuật dễ viết chương trình để nhanh chóng có được kết quả, thời gian thực hiện chương trình không được đề cao vì dù sao thì chương trình đó cũng chỉ sử dụng một vài lần mà thôi.
Tuy nhiên khi một chương trình được sử dụng nhiều lần thì thì yêu cầu tiết kiệm thời gian thực hiện chương trình lại rất quan trọng đặc biệt đối với những chương trình mà khi thực hiện cần dữ liệu nhập lớn do đó yêu cầu (3) sẽ được xem xét một cách kĩ càng. Ta gọi nó là hiệu quả thời gian thực hiện của giải thuật.
II. THỜI GIAN THỰC HIỆN CỦA CHƯƠNG TRÌNH
Một phương pháp để xác định hiệu quả thời gian thực hiện của một giải thuật là lập trình nó và đo lường thời gian thực hiện của hoạt động trên một máy tính xác định đối với tập hợp được chọn lọc các dữ liệu vào. Thời gian thực hiện không chỉ phụ thuộc vào giải thuật mà còn phụ thuộc vào tập các chỉ thị của máy tính, chất lượng của máy tính và kĩ xảo của người lập trình. Sự thi hành cũng có thể điều chỉnh để thực hiện tốt trên tập đặc biệt các dữ liệu vào được chọn. Ðể vượt qua các trở ngại này, các nhà khoa học máy tính đã chấp nhận tính phức tạp của thời gian được tiếp cận như một sự đo lường cơ bản sự thực thi của giải thuật. Thuật ngữ tính hiệu quả sẽ đề cập đến sự đo lường này và đặc biệt đối với sự phức tạp thời gian trong trường hợp xấu nhất.
Thời gian thực hiện chương trình.
Thời gian thực hiện một chương trình là một hàm của kích thước dữ liệu vào, ký hiệu T(n) trong đó n là kích thước (độ lớn) của dữ liệu vào. Chương trình tính tổng của n số có thời gian thực hiện là T(n) = cn trong đó c là một hằng số. Thời gian thực hiện chương trình là một hàm không âm, tức là T(n) ≥ 0 với mọi n ≥ 0.
Thời gian thực hiện một chương trình là một hàm của kích thước dữ liệu vào, ký hiệu T(n) trong đó n là kích thước (độ lớn) của dữ liệu vào. Chương trình tính tổng của n số có thời gian thực hiện là T(n) = cn trong đó c là một hằng số. Thời gian thực hiện chương trình là một hàm không âm, tức là T(n) ≥ 0 với mọi n ≥ 0.
Ðơn vị đo thời gian thực hiện.
Ðơn vị của T(n) không phải là đơn vị đo thời gian bình thường như giờ, phút giây… mà thường được xác định bởi số các lệnh được thực hiện trong một máy tính lý tưởng. Khi ta nói thời gian thực hiện của một chương trình là T(n) = Cn thì có nghĩa là chương trình ấy cần Cn chỉ thị thực thi.
Ðơn vị của T(n) không phải là đơn vị đo thời gian bình thường như giờ, phút giây… mà thường được xác định bởi số các lệnh được thực hiện trong một máy tính lý tưởng. Khi ta nói thời gian thực hiện của một chương trình là T(n) = Cn thì có nghĩa là chương trình ấy cần Cn chỉ thị thực thi.
Thời gian thực hiện trong trường hợp xấu nhất.
Nói chung thì thời gian thực hiện chương trình không chỉ phụ thuộc vào kích thước mà còn phụ thuộc vào tính chất của dữ liệu vào. Nghĩa là dữ liệu vào có cùng kích thước nhưng thời gian thực hiện chương trình có thể khác nhau. Chẳng hạn chương trình sắp xếp dãy số nguyên tăng dần, khi ta cho vào dãy có thứ tự thì thời gian thực hiện khác với khi ta cho vào dãy chưa có thứ tự, hoặc khi ta cho vào một dãy đã có thứ tự tăng thì thời gian thực hiện cũng khác so với khi ta cho vào một dãy đã có thứ tự giảm. Vì vậy thường ta coi T(n) là thời gian thực hiện chương trình trong trường hợp xấu nhất trên dữ liệu vào có kích thước n, tức là: T(n) là thời gian lớn nhất để thực hiện chương trình đối với mọi dữ liệu vào có cùng kích thước n.
Nói chung thì thời gian thực hiện chương trình không chỉ phụ thuộc vào kích thước mà còn phụ thuộc vào tính chất của dữ liệu vào. Nghĩa là dữ liệu vào có cùng kích thước nhưng thời gian thực hiện chương trình có thể khác nhau. Chẳng hạn chương trình sắp xếp dãy số nguyên tăng dần, khi ta cho vào dãy có thứ tự thì thời gian thực hiện khác với khi ta cho vào dãy chưa có thứ tự, hoặc khi ta cho vào một dãy đã có thứ tự tăng thì thời gian thực hiện cũng khác so với khi ta cho vào một dãy đã có thứ tự giảm. Vì vậy thường ta coi T(n) là thời gian thực hiện chương trình trong trường hợp xấu nhất trên dữ liệu vào có kích thước n, tức là: T(n) là thời gian lớn nhất để thực hiện chương trình đối với mọi dữ liệu vào có cùng kích thước n.
III. TỶ SUẤT GIA TĂNG VÀ ĐỘ PHỨC TẠP CỦA GIẢI THUẬT
Tỷ suất tăng
Ta nói rằng hàm không âm T(n) có tỷ suất tăng (growth rate) f(n) nếu tồn tại các hằng số C và sao cho T(n) ≤ Cf(n) với mọi
sao cho T(n) ≤ Cf(n) với mọi  . Ta có thể chứng minh được rằng “Cho một hàm không âm T(n) bất kỳ, ta luôn tìm được tỷ suất tăng f(n) của nó”.
. Ta có thể chứng minh được rằng “Cho một hàm không âm T(n) bất kỳ, ta luôn tìm được tỷ suất tăng f(n) của nó”.
Giả sử T(0) = 1, T(1) = 4 và tổng quát . Ðặt
. Ðặt = 1 và C = 4 thì với mọi n ≥1 chúng ta dễ dàng chứng minh được rằng
= 1 và C = 4 thì với mọi n ≥1 chúng ta dễ dàng chứng minh được rằng với mọi n ≥ 1, tức là tỷ suất tăng của T(n) là
với mọi n ≥ 1, tức là tỷ suất tăng của T(n) là .
.
Tỷ suất tăng của hàm . Thực vậy, cho
. Thực vậy, cho = 0 và C = 5 ta dễ dàng chứng minh rằng với mọi n ≥ 0 thì
= 0 và C = 5 ta dễ dàng chứng minh rằng với mọi n ≥ 0 thì
Ta nói rằng hàm không âm T(n) có tỷ suất tăng (growth rate) f(n) nếu tồn tại các hằng số C và
Giả sử T(0) = 1, T(1) = 4 và tổng quát
Tỷ suất tăng của hàm
Khái niệm độ phức tạp của giải thuật
Giả sử ta có hai giải thuật P1 và P2 với thời gian thực hiện tương ứng là (với tỷ suất tăng là
(với tỷ suất tăng là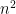 ) và
) và (với tỷ suất tăng là n3). Giải thuật nào sẽ thực hiện nhanh hơn? Câu trả lời phụ thuộc vào kích thước dữ liệu vào. Với n < 20 thì P2 sẽ nhanh hơn P1 (T2<T1), do hệ số của
(với tỷ suất tăng là n3). Giải thuật nào sẽ thực hiện nhanh hơn? Câu trả lời phụ thuộc vào kích thước dữ liệu vào. Với n < 20 thì P2 sẽ nhanh hơn P1 (T2<T1), do hệ số của nhỏ hơn hệ số của
nhỏ hơn hệ số của (5<100). Nhưng khi n > 20 thì ngược lại do số mũ của
(5<100). Nhưng khi n > 20 thì ngược lại do số mũ của nhỏ hơn số mũ của
nhỏ hơn số mũ của (2<3). Ở đây chúng ta chỉ nên quan tâm đến trường hợp n>20 vì khi n<20 thì thời gian thực hiện của cả P1 và P2 đều không lớn và sự khác biệt giữa T1 và T2 là không đáng kể.
(2<3). Ở đây chúng ta chỉ nên quan tâm đến trường hợp n>20 vì khi n<20 thì thời gian thực hiện của cả P1 và P2 đều không lớn và sự khác biệt giữa T1 và T2 là không đáng kể.
Như vậy một cách hợp lý là ta xét tỷ suất tăng của hàm thời gian thực hiện chương trình thay vì xét chính bản thân thời gian thực hiện.
Cho một hàm T(n), T(n) gọi là độ phức tạp f(n) nếu tồm tại các hằng C, sao cho
sao cho với mọi
với mọi (tức là T(n) có tỷ suất gia tăng là f(n)) và ký hiệu là O(f(n)). (“ô của f(n)”)
(tức là T(n) có tỷ suất gia tăng là f(n)) và ký hiệu là O(f(n)). (“ô của f(n)”)
 có tỷ suất tăng là
có tỷ suất tăng là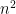 nên
nên là
là
Giả sử ta có hai giải thuật P1 và P2 với thời gian thực hiện tương ứng là
Như vậy một cách hợp lý là ta xét tỷ suất tăng của hàm thời gian thực hiện chương trình thay vì xét chính bản thân thời gian thực hiện.
Cho một hàm T(n), T(n) gọi là độ phức tạp f(n) nếu tồm tại các hằng C,
Chú ý: O(C.f(n))=O(f(n)) với C là hằng số. Ðặc biệt O(C) = O(1)
Nói cách khác độ phức tạp tính toán của giải thuật là một hàm chặn trên của hàm thời gian. Vì hằng nhân tử C trong hàm chặn trên không có ý nghĩa nên ta có thể bỏ qua vì vậy hàm thể hiện độ phức tạp có các dạng thường gặp sau: . Ba hàm cuối cùng ta gọi là dạng hàm mũ, các hàm khác gọi là hàm đa thức. Một giải thuật mà thời gian thực hiện có độ phức tạp là một hàm đa thức thì chấp nhận được tức là có thể cài đặt để thực hiện, còn các giải thuật có độ phức tạp hàm mũ thì phải tìm cách cải tiến giải thuật.
. Ba hàm cuối cùng ta gọi là dạng hàm mũ, các hàm khác gọi là hàm đa thức. Một giải thuật mà thời gian thực hiện có độ phức tạp là một hàm đa thức thì chấp nhận được tức là có thể cài đặt để thực hiện, còn các giải thuật có độ phức tạp hàm mũ thì phải tìm cách cải tiến giải thuật.
Chú ý: trong logn ta không cần quan tâm cơ số của nó vì với b>0. (Quy tắc bỏ hệ số sẽ đề cập trong Phần sau)
với b>0. (Quy tắc bỏ hệ số sẽ đề cập trong Phần sau)

